200以上 関数 の 解き方 254162-関数の解き方 例題

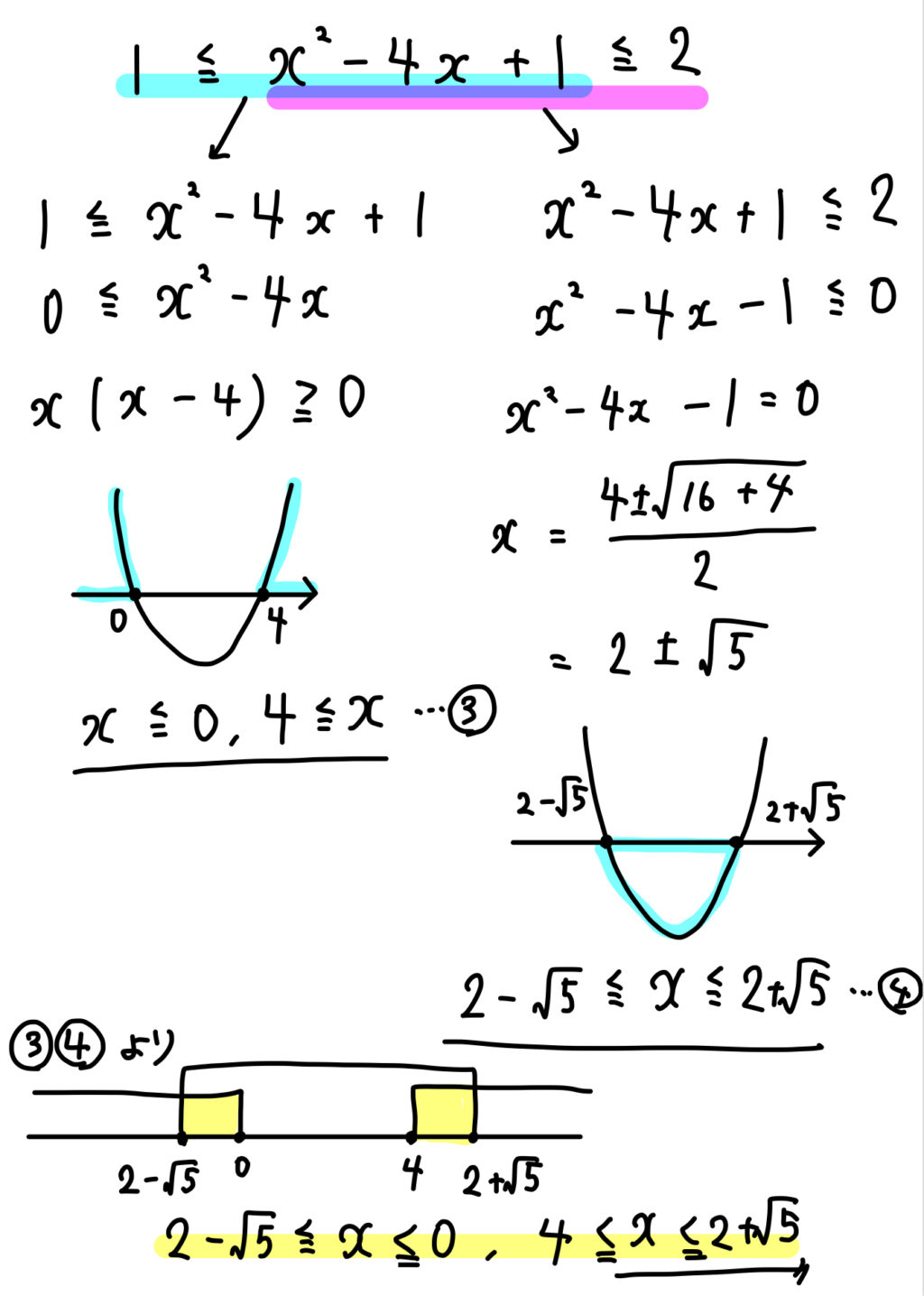
高校数学 絶対値付き2次不等式の解法 受験の月

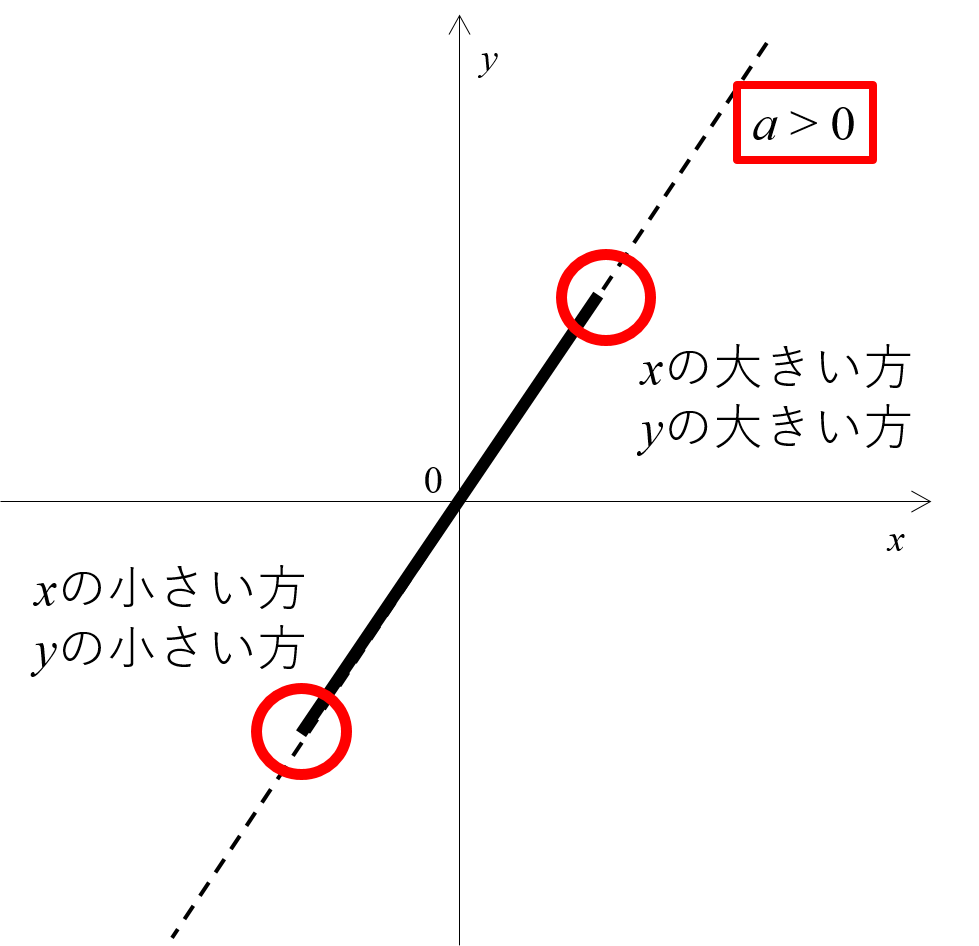
指数に未知数を含む不等式の解き方です。 まとまっている数を置き換えして解くのは方程式の場合と同じですが、 不等式は大小関係でもあるのでグラフを利用すると簡単に解ける問題が多いです。 指数関数のグラフは底の大きさでふた通り わかりやすく一次関数の解き方を解説 直線の式を求めるときはいつでもy=axb ほんとこれだけ覚えてください。笑 直線の式とか、一次関数の式と言われたら問題の下にまず y=axb と書いてください。 一次関数 式 という単語が出たらすぐ 「y=axb」 です。 これを100回は口に出して

関数の解き方 例題

関数の解き方 例題- vlookup関数の使い方は、視線の動きと「セリフ」を合わせた覚え方にすると、excel（エクセル）初心者さんも怖がらずに使えるようになります！ vlookupの使い方初心者さんのためのexcel関数解説 目次へ ページ上部へ エラーを表示しない iferror関数 iferror関数を使えば、「ゼロで割っている」の 二次関数の解き方を徹底解説 96%が知らない、元偏差値413でE判定の劣等生が、一切塾や予備校に通わずたった2ヶ月で偏差値70に！ 阪大理系に現役合格した禁断の合格法 この広告は、90日以上更新していないブログに表示しています。

３次方程式まとめ 解き方 因数分解 解と係数の関係 理系ラボ

 数学の疑問 部分積分の解き方とコツ。どっちを微分するか判断するポイントとは？ Tooda Yuuto 18年3月24日 / 19年9月9日 関数 \(f(x),g(x)\) とそれらを微分した \(f'(x),g'(x)\) に対して成立する以下の公式を、 部分積分 と言います。 （英語では Integration by parts） 例えば $\displaystyle \int x \sin{x}\ dx$ を更新日時 全射と単射 行き先の候補となるどんな元 y y y を持ってきても f (x) = y f(x)=y f (x) = y となる x x x が存在するとき， f (x) f(x) f (x) は全射である と言う。 「 f (x) = f (y) f(x)=f(y) f (x) = f 二次関数の最大最小の解き方2つのコツとは？場合分け 判別式dとは？公式・4分のdの意味・いつ使うかわかりやすく解説します スポンサーリンク 関連記事はこちら 三角比の相互関係の公式4つって？証明・覚え方・応用問題6選を解説 指数法則とは？公式の

これら2つは途中まで同じ計算を行いますが、計算のゴールが変わってきます。 不定積分は「微分したら \(f(x)\) になるような 関数を求めること 」がゴール 定積分は「関数 \(f(x)\) を \(a\) から \(b\) の範囲で積分し、 値の差（面積）を求めること 」がゴール という違いがあります。 関数方程式の解き方のコツまとめ このページで扱ったコツです。 解を予想して代入して確かめる（十分性）のも重要。 連続性は仮定されているか導くことができる場合が多い。 まずは適当に代入して f (0) f(0) f (0) を求める。 整数→有理数の流れで考える。 数学オリンピックでは，関数中学3年生の数学関数グラフの問題の解き方（基本～発展） 今回は『関数 ＝ y ＝ a x 2 』のグラフの問題の解き方をお伝えしていきます。 基本的な内容から発展までお伝えしていきます。 Contents 1 関数 ＝ y ＝ a x 2 グラフの問題の解き方（基本

関数の解き方 例題のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	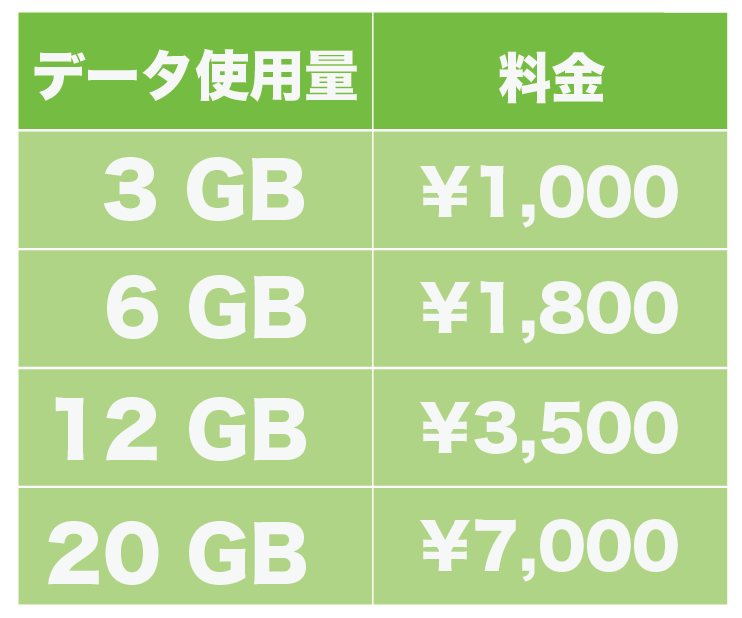高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	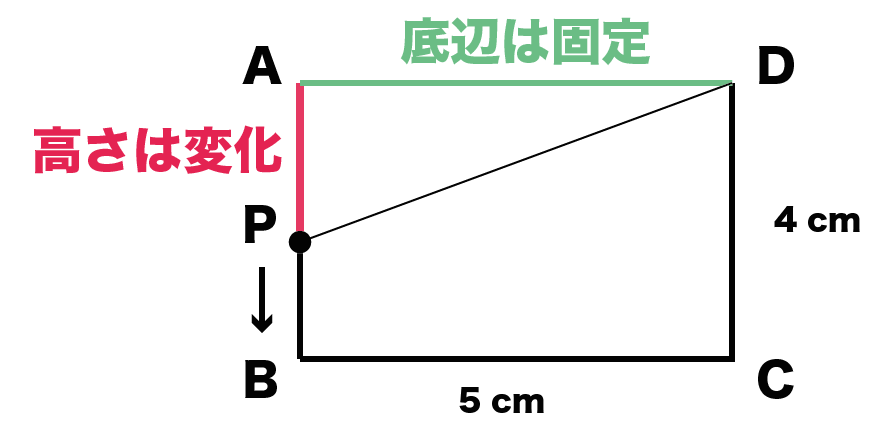高校数学で学習する連立方程式の解き方まとめ 数スタ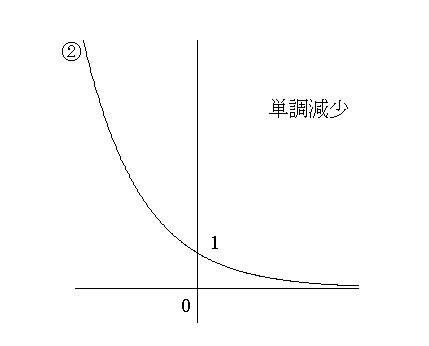
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ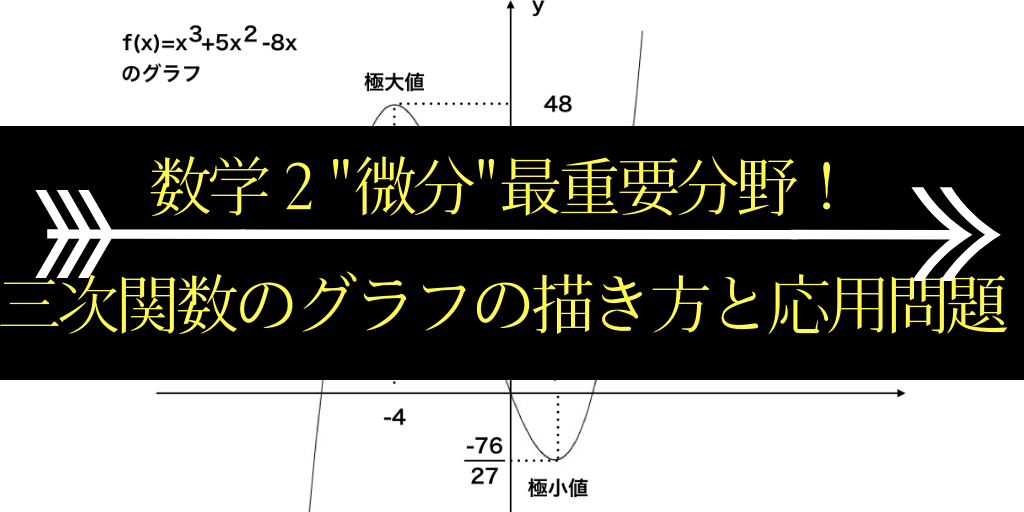
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	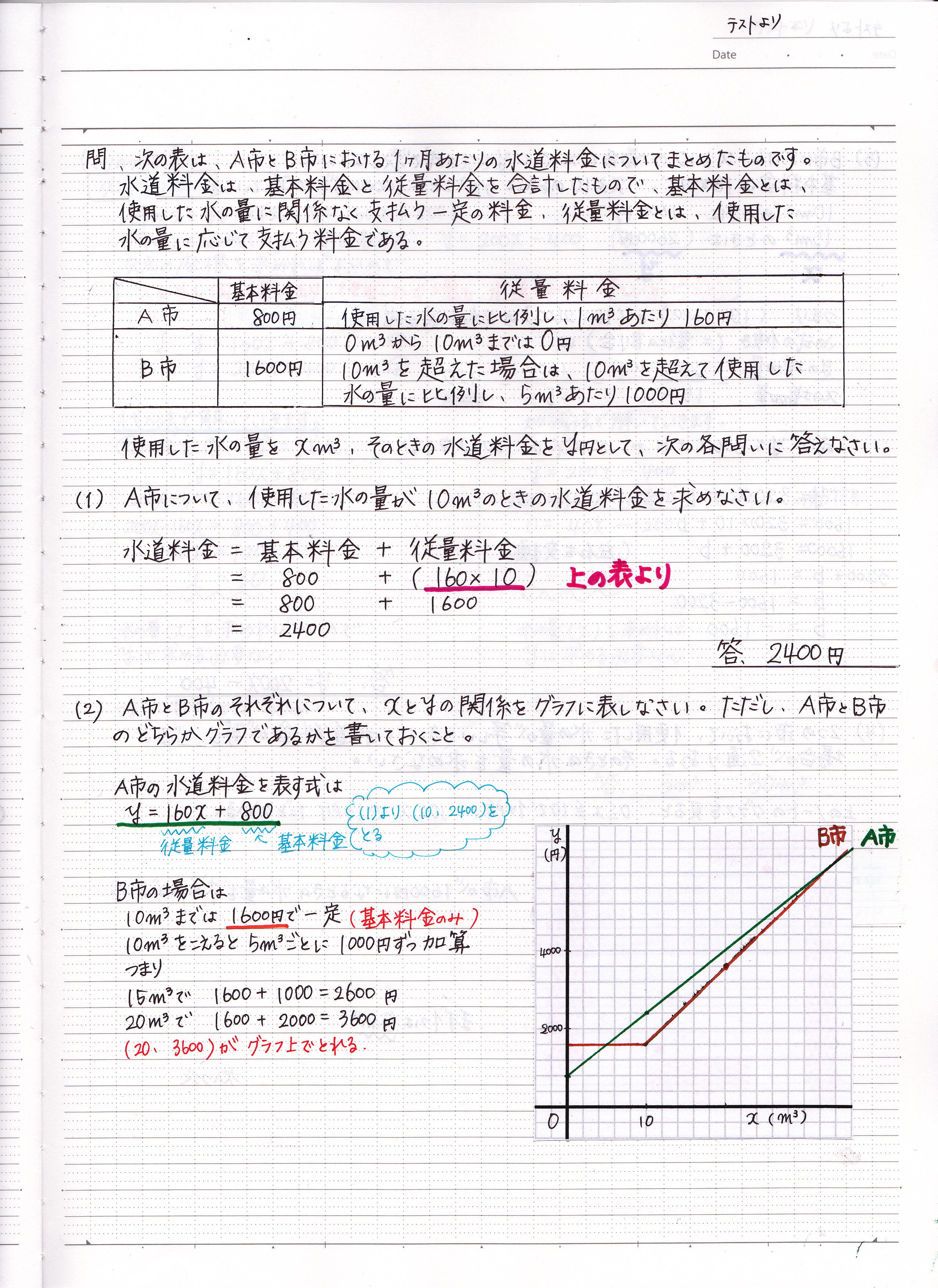高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	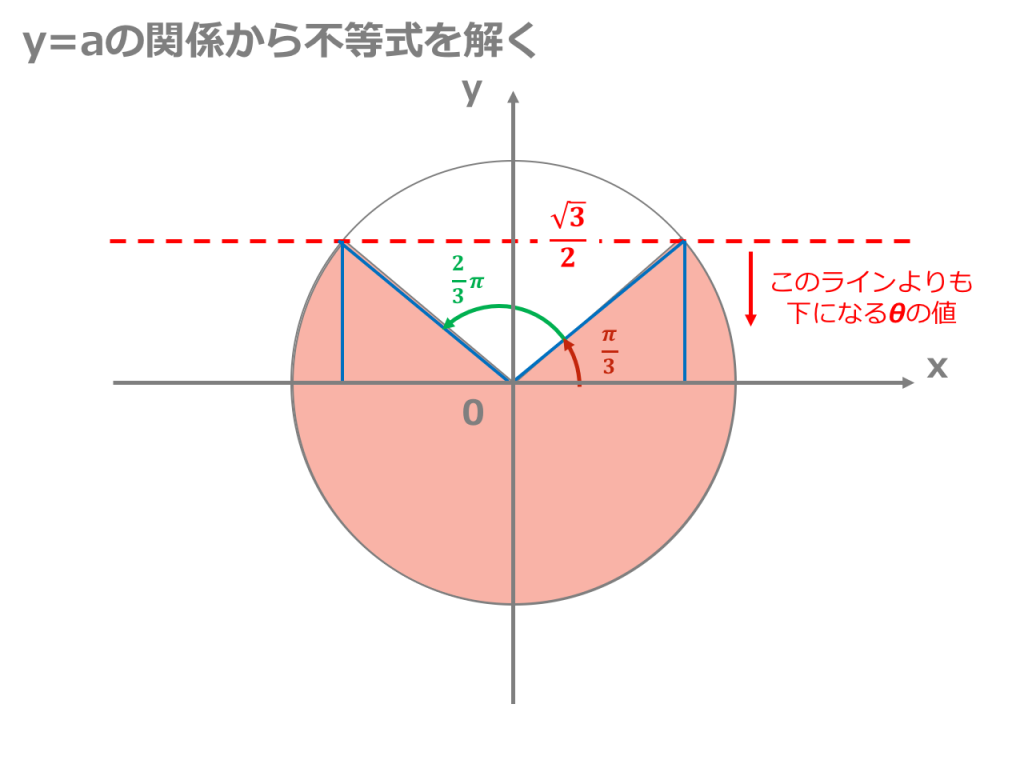高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ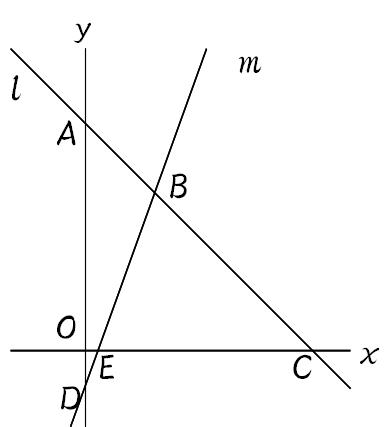
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ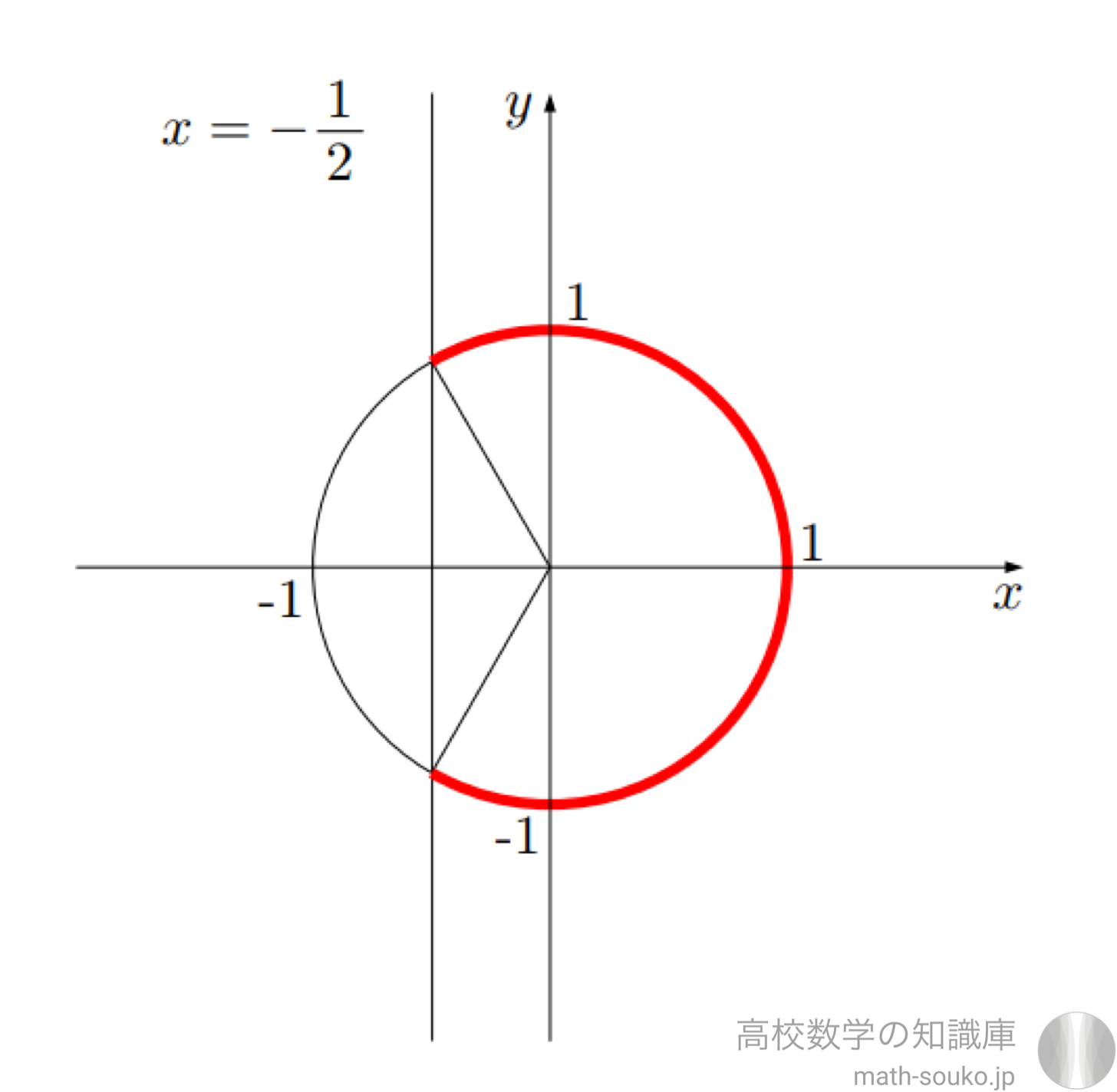
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ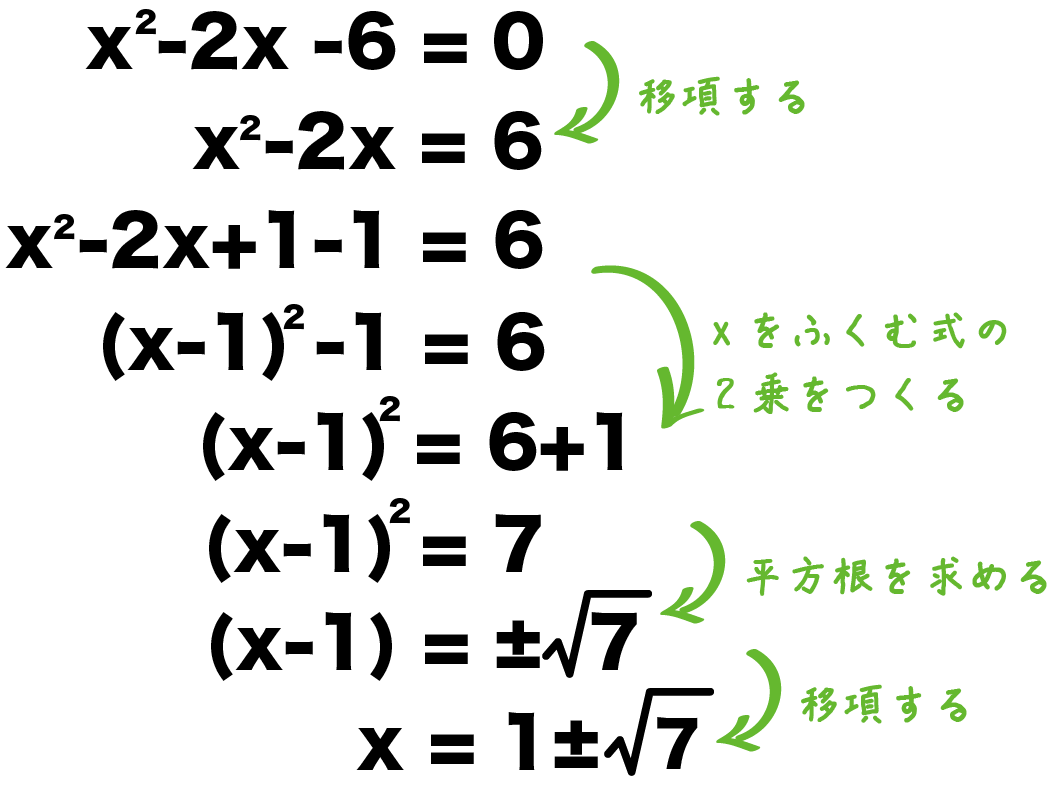
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	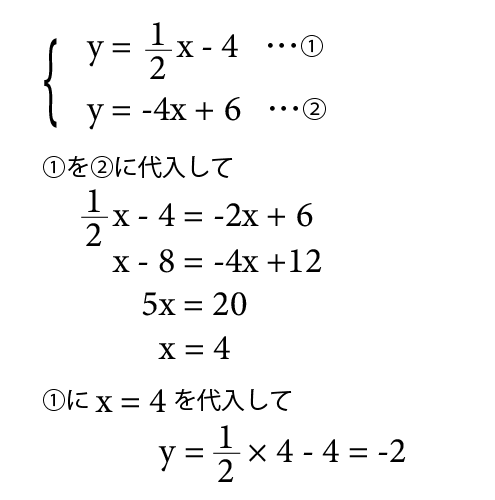高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	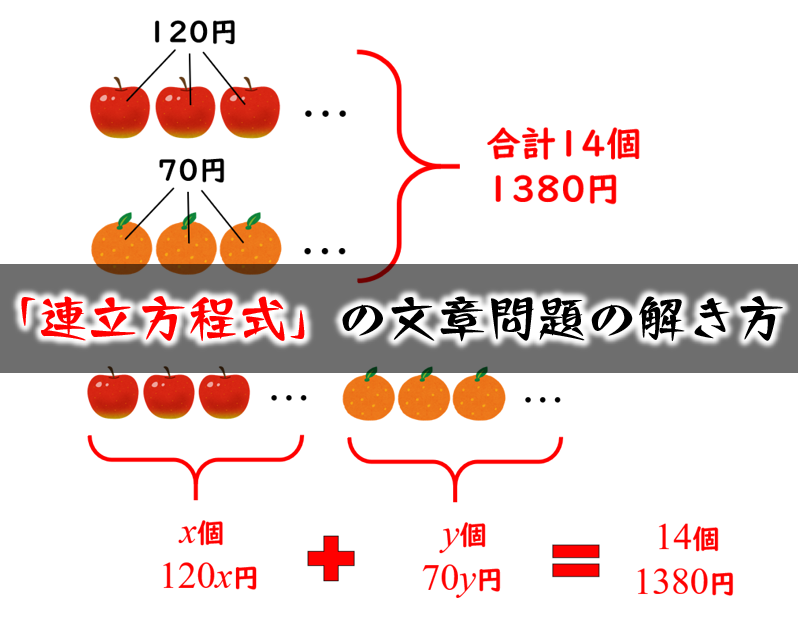高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ
高校数学で学習する連立方程式の解き方まとめ 数スタ	高校数学で学習する連立方程式の解き方まとめ 数スタ

三角関数の合成と最大値最小値問題の解き方 三角関数の合成は最大値や最小値を求める問題の解き方の1つです。三角方程式に使うだけではありません。 三角比では2次関数に置きかえて解くことが多かった最大、最小 最近の投稿記事 21年度共通テスト数学2B（選択問題）の解説;平方完成の手順 平方完成は以下の手順で行うとよい。 ① x を含む項だけ、 x2 の係数でくくる ② x の係数を半分にして、2乗を足し引きする ③ 因数分解する ④ 分配法則を用いる ⑤ 定数項を計算する 例えば、3 x2 12 x 6を平方完成すると、 となる。

Incoming Term: 関数の解き方 例題, 関数の解き方,